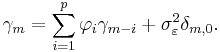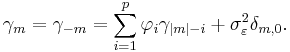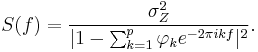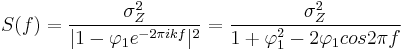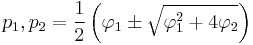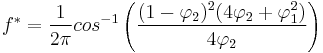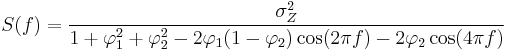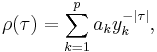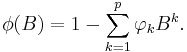Autoregressive model
In statistics and signal processing, an autoregressive (AR) model is a type of random process which is often used to model and predict various types of natural phenomena. The autoregressive model is one of a group of linear prediction formulas that attempt to predict an output of a system based on the previous outputs.
Contents |
Definition
The notation AR(p) indicates an autoregressive model of order p. The AR(p) model is defined as
where  are the parameters of the model,
are the parameters of the model,  is a constant (often omitted for simplicity) and
is a constant (often omitted for simplicity) and 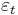 is white noise.
is white noise.
An autoregressive model can thus be viewed as the output of an all-pole infinite impulse response filter whose input is white noise.
Some constraints are necessary on the values of the parameters of this model in order that the model remains wide-sense stationary. For example, processes in the AR(1) model with |φ1| ≥ 1 are not stationary. More generally, for an AR(p) model to be wide-sense stationary, the roots of the polynomial 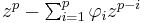 must lie within the unit circle, i.e., each root
must lie within the unit circle, i.e., each root 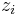 must satisfy
must satisfy 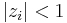 .
.
Example: An AR(1)-process
An AR(1)-process is given by:
where 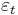 is a white noise process with zero mean and variance
is a white noise process with zero mean and variance 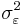 . (Note: The subscript on
. (Note: The subscript on 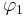 has been dropped.) The process is wide-sense stationary if
has been dropped.) The process is wide-sense stationary if 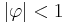 since it is obtained as the output of a stable filter whose input is white noise. (If
since it is obtained as the output of a stable filter whose input is white noise. (If 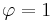 then
then 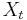 has infinite variance, and is therefore not wide sense stationary.) Consequently, assuming
has infinite variance, and is therefore not wide sense stationary.) Consequently, assuming 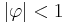 , the mean
, the mean 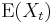 is identical for all values of t. If the mean is denoted by
is identical for all values of t. If the mean is denoted by  , it follows from
, it follows from
that
and hence
In particular, if 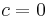 , then the mean is 0.
, then the mean is 0.
The variance is
where 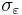 is the standard deviation of
is the standard deviation of 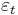 . This can be shown by noting that
. This can be shown by noting that
and then by noticing that the quantity above is a stable fixed point of this relation.
The autocovariance is given by
It can be seen that the autocovariance function decays with a decay time (also called time constant) of 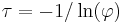 [to see this, write
[to see this, write 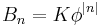 where
where  is independent of
is independent of  . Then note that
. Then note that 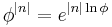 and match this to the exponential decay law
and match this to the exponential decay law 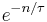 ].
].
The spectral density function is the Fourier transform of the autocovariance function. In discrete terms this will be the discrete-time Fourier transform:
This expression is periodic due to the discrete nature of the 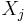 , which is manifested as the cosine term in the denominator. If we assume that the sampling time (
, which is manifested as the cosine term in the denominator. If we assume that the sampling time (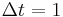 ) is much smaller than the decay time (
) is much smaller than the decay time ( ), then we can use a continuum approximation to
), then we can use a continuum approximation to 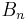 :
:
which yields a Lorentzian profile for the spectral density:
where 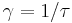 is the angular frequency associated with the decay time
is the angular frequency associated with the decay time  .
.
An alternative expression for 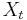 can be derived by first substituting
can be derived by first substituting 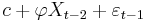 for
for 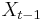 in the defining equation. Continuing this process N times yields
in the defining equation. Continuing this process N times yields
For N approaching infinity, 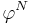 will approach zero and:
will approach zero and:
It is seen that 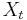 is white noise convolved with the
is white noise convolved with the 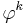 kernel plus the constant mean. If the white noise
kernel plus the constant mean. If the white noise 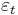 is a Gaussian process then
is a Gaussian process then 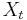 is also a Gaussian process. In other cases, the central limit theorem indicates that
is also a Gaussian process. In other cases, the central limit theorem indicates that 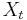 will be approximately normally distributed when
will be approximately normally distributed when  is close to one.
is close to one.
Calculation of the AR parameters
There are many ways to estimate the coefficients: the OLS procedure, method of moments (through Yule Walker equations),MCMC.
The AR(p) model is given by the equation
It is based on parameters 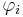 where i = 1, ..., p. There is a direct correspondence between these parameters and the covariance function of the process, and this correspondence can be inverted to determine the parameters from the autocorrelation function (which is itself obtained from the covariances). This is done using the Yule-Walker equations.
where i = 1, ..., p. There is a direct correspondence between these parameters and the covariance function of the process, and this correspondence can be inverted to determine the parameters from the autocorrelation function (which is itself obtained from the covariances). This is done using the Yule-Walker equations.
Yule-Walker equations
The Yule-Walker equations are the following set of equations.
where m = 0, ... , p, yielding p + 1 equations. 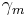 is the autocorrelation function of X,
is the autocorrelation function of X, 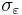 is the standard deviation of the input noise process, and
is the standard deviation of the input noise process, and 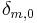 is the Kronecker delta function.
is the Kronecker delta function.
Because the last part of the equation is non-zero only if m = 0, the equation is usually solved by representing it as a matrix for m > 0, thus getting equation
solving all  . For m = 0 we have
. For m = 0 we have
which allows us to solve 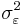 .
.
The above equations (the Yule-Walker equations) provide one route to estimating the parameters of an AR(p) model, by replacing the theoretical covariances with estimated values. One way of specifying the estimated covariances is equivalent to a calculation using least squares regression of values Xt on the p previous values of the same series.
Another usage is calculating the first p+1 elements 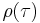 of the auto-correlation function. The full auto-correlation function can then be derived by recursively calculating [1]
of the auto-correlation function. The full auto-correlation function can then be derived by recursively calculating [1]
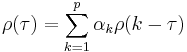
- Examples for some Low-order AR(p) processes
- p=1
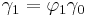
- Hence
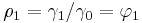
- p=2
- The Yule-Walker equations for an AR(2) process are
- Remember that
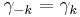
- Using the first equation yields
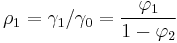
- Using the recursion formula yields
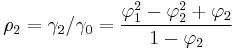
- The Yule-Walker equations for an AR(2) process are
- p=1
Derivation
The equation defining the AR process is
Multiplying both sides by Xt − m and taking expected value yields
Now, ![\operatorname{E}[X_t X_{t-m}] = \gamma_m](/2012-wikipedia_en_all_nopic_01_2012/I/eba933925087c12ad77002114e86b5e4.png) by definition of the autocorrelation function. The values of the noise function are independent of each other, and Xt − m is independent of εt where m is greater than zero. For m > 0, E[εtXt − m] = 0. For m = 0,
by definition of the autocorrelation function. The values of the noise function are independent of each other, and Xt − m is independent of εt where m is greater than zero. For m > 0, E[εtXt − m] = 0. For m = 0,
Now we have, for m ≥ 0,
Furthermore,
which yields the Yule-Walker equations:
for m ≥ 0. For m < 0,
Spectrum
The power spectral density of an AR(p) process with noise variance 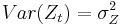 is[1]
is[1]
AR(0)
For white noise (AR(0))
AR(1)
For AR(1)
- If
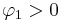 there is a single spectral peak at f=0, often referred to as red noise. As
there is a single spectral peak at f=0, often referred to as red noise. As 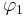 becomes nearer 1, there is stronger power at low frequencies, i.e. larger time lags.
becomes nearer 1, there is stronger power at low frequencies, i.e. larger time lags. - If
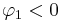 there is a minimum at f=0, often referred to as blue noise
there is a minimum at f=0, often referred to as blue noise
AR(2)
AR(2) processes can be split into three groups depending on the characteristics of their roots:
- When
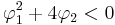 , the process has a pair of complex-conjugate roots, creating a mid-frequency peak at:
, the process has a pair of complex-conjugate roots, creating a mid-frequency peak at:
Otherwise the process has real roots, and:
- When
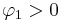 it acts as a low-pass filter on the white noise with a spectral peak at
it acts as a low-pass filter on the white noise with a spectral peak at 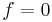
- When
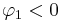 it acts as a high-pass filter on the white noise with a spectral peak at
it acts as a high-pass filter on the white noise with a spectral peak at 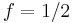 .
.
The process is stable when the roots are within the unit circle, or equivalently when the coefficients are in the triangle 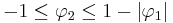 .
.
The full PSD function can be expressed in real form as:
Characteristic polynomial
Auto-correlation function of an AR(p) process can be expressed as
where 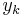 are the roots of the polynomial
are the roots of the polynomial
Auto-correlation function of an AR(p) process is a sum of decaying exponential.
- Each real root contributes a component to the auto-correlation function that decays exponentially.
- Similarly, each pair of complex conjugate roots contributes an exponentially damped oscillation.
Implementations in statistics packages
See also
- Moving average model
- Autoregressive moving average model
- Predictive analytics
- Linear predictive coding
Notes
- ^ a b Von Storch, H.; F. W Zwiers (2001). Statistical analysis in climate research. Cambridge Univ Pr. ISBN 0521012309.
- ^ "Fit Autoregressive Models to Time Series"
References
- Mills, Terence C. (1990) Time Series Techniques for Economists. Cambridge University Press
- Percival, Donald B. and Andrew T. Walden. (1993) Spectral Analysis for Physical Applications. Cambridge University Press
- Pandit, Sudhakar M. and Wu, Shien-Ming. (1983) Time Series and System Analysis with Applications. John Wiley & Sons
- Yule, G. Udny (1927) "On a Method of Investigating Periodicities in Disturbed Series, with Special Reference to Wolfer's Sunspot Numbers", Philosophical Transactions of the Royal Society of London, Ser. A, Vol. 226, 267–298.]
- Walker, Gilbert (1931) "On Periodicity in Series of Related Terms", Proceedings of the Royal Society of London, Ser. A, Vol. 131, 518–532.
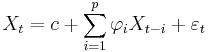
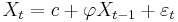
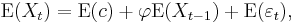
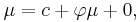
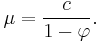
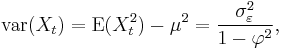
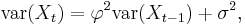
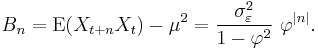
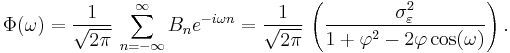
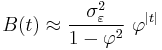
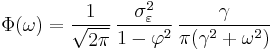
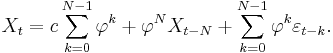
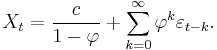
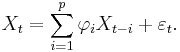
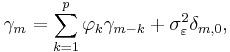
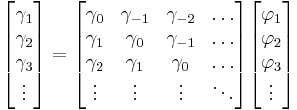
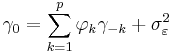
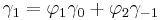
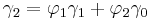
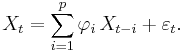
![\operatorname{E}[X_t X_{t-m}] = \operatorname{E}\left[\sum_{i=1}^p \varphi_i\,X_{t-i} X_{t-m}\right]%2B \operatorname{E}[\varepsilon_t X_{t-m}].](/2012-wikipedia_en_all_nopic_01_2012/I/33913fbece0498dfea2a9c8ab88eed2d.png)
![\operatorname{E}[\varepsilon_t X_{t}]
= \operatorname{E}\left[\varepsilon_t \left(\sum_{i=1}^p \varphi_i\,X_{t-i}%2B \varepsilon_t\right)\right]
= \sum_{i=1}^p \varphi_i\, \operatorname{E}[\varepsilon_t\,X_{t-i}] %2B \operatorname{E}[\varepsilon_t^2]
= 0 %2B \sigma_\varepsilon^2,](/2012-wikipedia_en_all_nopic_01_2012/I/e956d1fc426c3ace8e759d4f592256d8.png)
![\gamma_m = \operatorname{E}\left[\sum_{i=1}^p \varphi_i\,X_{t-i} X_{t-m}\right] %2B \sigma_\varepsilon^2 \delta_{m,0}.](/2012-wikipedia_en_all_nopic_01_2012/I/0e9a4ce5b3c5f27a773bae9a2cccbc2e.png)
![\operatorname{E}\left[\sum_{i=1}^p \varphi_i\,X_{t-i} X_{t-m}\right]
= \sum_{i=1}^p \varphi_i\,\operatorname{E}[X_{t} X_{t-m%2Bi}]
= \sum_{i=1}^p \varphi_i\,\gamma_{m-i},](/2012-wikipedia_en_all_nopic_01_2012/I/a8c4bfab4d9d5e41ef57f76e5fbf259d.png)